Kompetensi Dasar
3.1 Menerapkan konsep torsi, momen inersia, titik berat, dan momentum sudut pada benda tegar (statis dan dinamis) dalam kehidupan sehari-hari misalnya dalam olahraga
4.1 Membuat karya yang menerapkan konsep titik berat dan kesetimbangan benda tegar
Momen gaya (Torsi)
Momen gaya atau torsi adalah kecenderungan suatu benda untuk memutar benda pada suatu poros. Torsi dilambangkan dengan τ (dibaca tau). Secara sistematis, torsi merupakan hasil kali silang antara lengan torsi dan vektor gaya dengan satuan Nm. Torsi merupakan besaran vektor sehingga dapat bernilai positif maupun negatif. Torsi akan bernilai positif jika arah putarannya searah jarum jam dan akan bernilai negatif jika arah putarannya berlawanan arah jarum jam. Penerapan torsi dalam kehidupan sehari-hari ialah ketika kita membuka pintu, memasang baut dan menimba air dengan katrol.
τ = F x r
τ = F r sin α
dengan,
τ = torsi atau momen gaya (Nm)
F = gaya (N)
r = lengan gaya (m)
α = sudut antara F dan r ( °)
Momen Inersia
Momen inersia adalah ukuran suatu kelembaman (kemalasan) suatu benda untuk berotasi pada porosnya. Secara sistematis, momen inersia merupakan hasil kali antara massa partikel dengan kuadrat jarak partikel terhadap porosnya. Besarnya sebuah momen inersia suatu benda itu bergantung terhadap beberapa faktornya, yaitu:
1. Massa benda atau partikel
2. Bentuk benda
3. Letak sumbu putar benda
4. Jarak ke sumbu putar benda
I = ∑ m r²
dengan,
I = momen inersia (kg m²)
m = massa benda atau partikel (kg)
r = jarak partikel terhadap porosnya (m)
Momen Inersia untuk berbagai bentuk benda adalah sebagai berikut.
Pada momen inersia, teorema sumbu sejajar atau teorema Huygens-Steiner dapat digunakan untuk menentukan momen inersia sebuah benda tegar terhadap sumbu tertentu, bila diketahui momen inersia suatu objek terhadap sumbu yang melalui pusat massa yang sejajar dengan sumbu pertama, serta jarak tegak lurus antara kedua sumbu tersebut.
Hubungan antara torsi dengan momen inersia dapat dituliskan sebagai berikut.
τ = I α
dengan,
τ = torsi atau momen gaya (Nm)
I = momen inersia (kg m²)
α = percepatan sudut (rad/s²)
Hukum Kekekalan Momentum Sudut
sumber gambar: physicsforums.com
Pernahkah kalian melihat seseorang bermain ice skating? Apa yang terjadi saat pemain ice skating merentangkan lengannya sambil berputar seperti pada gambar (a) dan apa yang akan terjadi setelah pemain ice skating melipat lengannya seperti gambar (b)?
Pemain ice skating berputar perlahan saat membentangkan lengannya. Ketika pemain melipat lengannya kecepatan putarannya bertambah, dan membentangkan kembali lengannya saat akan berhenti dari putaran. Pada kejadian ini berlaku hukum kekekalan momentum yaitu momentum sudut saat membentangkan sama dengan momentum sudut saat melipat tangannya. Secara sistematis dapat dituliskan sebagai berikut.
Energi Kinetik Rotasi
Setiap benda yang bergerak memiliki energi kinetik. Pada bab usaha dan energi sebelumnya, kalian sudah mempelajari energi kinetik pada gerak translasi yang besarnya:
Ek = ½ m v²
dengan,
m = massa benda (kg)
v = kecepatan gerak benda (m/s)
karena kecepatan linier sebuah benda, v = r. ω, maka:
Ek = ½ m (r ω)² = ½ m r² ω²
Karena m r² = I, maka pada saat berotasi, benda memiliki energi gerak yang disebut energi kinetik rotasi, yang besarnya:
Ek = ½ I ω²
Untuk sebuah benda yang menggelinding pada bidang datar, maka benda itu mengalami dua energi kinetik sekaligus, yaitu energi kinetik translasi dan energi kinetik rotasi seperti ilustrasi bi bawah ini.
Sehingga dirumuskan sebagai berikut.
Ek = Ek translasi + Ek rotasi
Ek = ½ I ω2 + ½ m v2
Usaha Pada Gerak Rotasi
Perhatikan gambar di bawah ini!
Usaha yang dilakukan oleh sebuah roda yang berotasi pada sumbu tetap dalam selang waktu Δt, sebuah titik pada roda tersebut menempuh sudut θ dan lintasan sejauh s. Usaha yang dilakukan gaya F adalah:
W = F . s
Karena s = r . θ dan τ = r . F, maka:
W = τ . θ
dengan:
W = usaha ( J)
τ = momen gaya (Nm2)
θ = sudut yang ditempuh
Usaha merupakan perubahan energi kinetik rotasi suatu benda yang dapat dituliskan sebagai berikut.
Gerak Menggelinding pada Bidang Datar
Gerak menggelinding terjadi saat sebuah benda mengalami dua macam gerakan secara bersamaan, yaitu gerak translasi dan gerak rotasi.
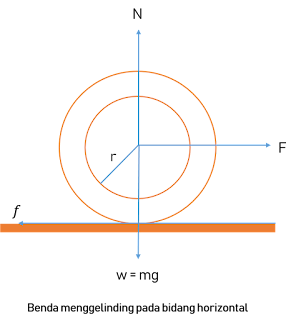
Perhatikan gambar berikut.
Sebuah bola bermassa m dan berjari-jari r menggelinding sepanjang bidang datar horizontal. Pada bola diberikan gaya sebesar F. Berapakah percepatan bola tersebut jika bola menggelinding tanpa gesekan? Jika bola menggelinding, maka bola tersebut bergerak secara translasi dan rotasi. Pada kedua macam gerak tersebut berlaku persamaan-persamaan berikut.
Untuk gerak translasi berlaku persamaan F – f = m a dan N – m g = 0
Untuk gerak rotasi berlaku persamaan ∑τ = I α
Karena bola menggelinding tanpa gesekan, maka harus ada gaya gesekan. Besarnya gaya gesekan pada sistem ini adalah sebagai berikut.
Untuk menentukan nilai percepatan pada bola yang menggelinding adalah sebagai berikut.
Gerak Menggelinding pada Bidang Miring
Sebuah bola yang menggelinding pada bidang miring akan mengalami gerak translasi dengan mengasumsikan semua gaya luar bekerja di pusat massa silinder. Menurut hukum Sir Isaac Newton:
a. Persamaan gerak dalam arah normal adalah N – mg cos θ = 0
b. Persamaan gerak sepanjang bidang miring adalah mg sin θ – f = ma
c. Gerak rotasi terhadap pusat massanya ∑τ = I α
Gaya normal N dan gaya berat mg tidak dapat menimbulkan rotasi terhadap titik pusat. Hal ini disebabkan garis kerja gaya melalui titik pusat, sehingga lengan momennya sama dengan nol. Persamaan yang berlaku adalah sebagai berikut.
Kesetimbangan Benda Tegar
Syarat terjadinya kesetimbangan benda tegar adalah sebagai berikut.
1. Resultan gaya yang bekerja pada benda adalah nol.
∑Fx = 0
∑Fy = 0
2. Resultan momen gaya (torsi) yang bekerja pada benda adalah nol.
∑𝛕 = 0
Titik Berat
Benda terdiri atas partikel-partikel yang masing-maing mempunyai berat. Resultan dari gaya berat partikel-partikel tersebut adalah berat benda (X0, Y0, Z0). Titik tangkap dari gaya berat disebut titik berat. Untuk menentukan titik berat suatu benda dapat dirumuskan sebagai berikut.
1. Titik Berat Benda Berbentuk Garis
2. Titik Berat Bidang Homogen
3. Titik Berat Benda Berongga Homogen
Macam-Macan Kesetimbangan
1. Kesetimbangan Stabil
Kesetimbangan Stabil adalah kesetimbangan yang dialami sebuah benda apabila benda tersebut dipengaruhi oleh gaya atau gangguan, namun benda tersebut akan kembali ke posisi semula.
Gambar di atas menunjukkan sebuah bola yang ditempatkan dalam bidang cekung. Ketika diberi gaya dan kemudian dihilangkan, kelereng akan kembali ke posisi semula.
2. Kesetimbangan Labil
Kesetimbangan labil adalah kesetimbangan yang dialami benda yang apabila diberikan gaya, benda tersebut tidak bisa kembali ke posisi semula, melainkan akan tetap diam pada posisi yang baru.
Pada gambar di atas menunjukkan sebuah bola yang ditempatkan di atas bidang cembung. Ketika diberi gaya dan kemudian dihilangkan, maka bola tidak akan pernah kembali ke posisi awalnya.
3. Kesetimbangan Indiferen
Kesetimbangan indeferen atau netral adalah kesetimbangan yang dialami benda yang apabila diberikan gaya, maka benda tersebut tidak mengalami perubahan titik berat benda.
Pada gambar di atas menunjukkan bola yang ditempatkan di atas sebuah bidang datar. Ketika diberi gaya dan kemudian dihilangkan, maka bola tersebut akan kembali diam pada kedudukan yang berbeda.
kesetimbangan benda tegar. dinamika rotasi kelas xii. soal-soal kesetimbangan benda tegar. fisika sma kelas xii. belajar fisika. kesetimbangan benda tegar kelas 11. ekanurain.





















0 comments